10. Zertan geratzen da egiaztatu nahi duzun hipotesia V eta N konstante mantentzen badira?

 

11. Zein esperientzia proposatuko zenuke hipotesi hori egiaztatzeko?

Irakasleak emango dizu esperientziaren emaitza, hau da, p/t grafikoa.

12. Zer ondorioztatzen duzu? Bete al da hipotesia?

Presioa tenperaturarekiko zuzenki proportzionala ateratzen ez dela ikusita, badirudi proposatutako hipotesia ez dela zuzena. Proposatu dugun hipotesia beteko balitz, hau da, p/t grafikoa jatorritik igaroko balitz, gasaren presioak p = 0 Pa izan beharko luke bere tenperatura t = 0 °C denean. Eta ez da hala gertatzen.
Zer egin dezakegu? Hipotesia baztertu? Ala bete dadin zerbait aldatzen saiatu? Zeren p eta t proportzionalak izatea guztiz logikoa baitirudi. Goazen, beraz, azken bide horretan saiatzera.

13. Lehengo p/t grafikoaren martxa ikusita, zein tenperaturatan izango litzateke zero gasaren presioa?

Beste gas-lagin bat hartzen badugu (N eta V desberdinak izango dira, orokorrean) eta t desberdinentzako p neurtzen badugu, p/t grafikoa ez da aurrekoa bezalakoa ateratzen, zure hipotesia betetzen delarik. Izan ere, hipotesiaren arabera V eta N desberdina duen gasaren p, t jakin batean, desberdina izango da, eta hala ateratzen da. Baina grafikoa desberdina izanik ere, aurrekoan bezala gas-lagin berri horren p zein t-n egingo litzatekeen zero kalkulatuz gero, zuk lortu duzun balioaren antzekoa ateratzen da, -273 °C alegia; hala atera zitzaion behintzat Gay-Lussac zientzialari frantziarrari, gasen presioa eta tenperaturaren arteko erlazioa ikertzen aritu zenean. Eta gauza bera gertatu zitzaion edozein gas-laginarekin.

	p(atm)	1. gasa (N1, V2)
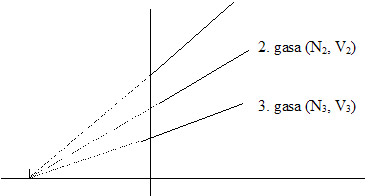
- 273			t(°C)

Beraz, badirudi t horretan edozein gasaren p zero egingo litzatekeela, berdin du zein den gasaren N edo V.

14. Posible izango al da tenperatura hori lortzea? Eta tenperatura horretatik jaistea?

Ez dirudi, ez, -273 °C-eko t lortzea posible denik. Zeren, nola egon daiteke presiorik egiten ez duen gasik? Eta are gehiago, tenperatura horren azpitik presioak negatiboa izan beharko zuen. Ez da posible.

Baina guk zure hipotesiarekin genuen arazoa konpondu nahian genbiltzan.

15. Zer gertatuko litzateke tenperatura-eskala aldatu eta eskala berriaren zeroa -273 °C-tan kokatuko bagenu? Zein tenperaturan egingo litzateke orduan zero edozein gasaren presioa? Beteko al litzateke orduan gure hasierako hipotesia?

Gay-Lussacen neurketa eta kalkuluetan oinarrituta, kimikariek tenperatura-eskalaren jatorria puntu horretara (-273 °C) eramanez, konturatu egin ziren p zero egiten dela T zero denean, hau da, p/T grafikoa jatorritik igarotzen den zuzena dela, p eta T zuzenki proportzionalak direla: proposatutako hipotesia bete egiten dela, alegia.
Tenperatura-eskala horri, tenperatura absolutua edo tenperatura termodinamikoa (T, ez t Celsius-eskalan neurtzen denean bezala) deitzen zaio. Jatorria, esan bezala, -273 °C-tan dago, eta unitatea Kelvin (K) deitzen da, hau da: 0 K = -273 °C.

Baieztatu duzun hipotesia Gay-Lussac-en bigarren legea da:
Gas batek egiten duen presioa tenperatura absolutuarekiko zuzenki proportzionala da, bolumena eta korpuskulu-kopurua konstante mantentzen badira:
p = k·T

16. Zein da tenperatura-eskala absolutua eta Celsius-eskalaren arteko erlazioa?

Eta zein da, bada, Gay-Lussac-en lehen legea? Ba V eta t-ren arteko erlazioa (p eta N konstanteak izanik) ezartzen duena. Izan ere, Gay-Lussacek erlazio hau p eta t-ren artekoa baino lehen ikertu zuen. Goazen gu ere erlazio hori ikertzera.

 

17. Nola geratzen da, zure hipotesiaren arabera, V eta t-ren arteko erlazioa, p eta N konstante mantenduz gero?

18. Zein muntaketa esperimentala egin daiteke erlazio hori baieztatzeko?

Egiaztapen esperimentala egiteko dauden zailtasun teknikoak ez dira samurrak. Gasaren tenperatura igotzen den heinean presioa konstante mantentzeko, gasari zabaltzeko aukera utzi behar zaio, baina ihes egin gabe. Gay-Lussacek 1.802. urtean lortu zuen lehen muntaketa egokia diseinatzea. Honetan, gasa zeukan ontzia merkurio tanta batez itxita zegoen hodi graduatuari lotuta zegoen. Hala, t igo ahala V-ren igoera ikusten zuen, eta p-ren konstantetasuna igoera minimoarekin desplazatzen zen merkurio tantak ziurtatzen zuen, hodi graduatua horizontalki kokatzen baitzen.

Zuk esperientzia bera egingo duzu, baina simulazio baten bitartez, interneten aurki dezakezun

http://perso.wanadoo.es/cpalacio/LeyCharles2.htm web orrian.

Bertan "Ley de Charles" klikatuz gero, U formako hodi graduatua aurkituko duzu. Hodiaren mutur bat itxita dago, eta bertan airea dago. Merkurioz mantentzen da itxita gas hori (gasaren N konstante mantenduko da, beraz), eta beste muturra irekia da. Gero, termometro batean kurtsorearen bitartez, hodian dagoen airearen tenperatura igo dezakezu; tenperatura igo ahala, airea zabaldu egiten da, eta hodian bolumen gehiago hartzen du.
Orduan arazo txiki bat sortzen da: U formako hodiaren bi aldeetan merkurioak maila desberdina hartzen du, alde batean gasak bultzatuta, eta beraz, gasaren p igo egiten da. Baina Hg- marka duen botoia sakatuz, merkurioa atera dezakezu hoditik, bi adarretan altuera bera izan arte, aireak berriro kanpoko eguratsaren p berreskuratu arte. Horrela ziurta dezakezu p konstante mantentzen dela t (eta V) igotzen diren bitartean.
Datuak sartuz, grafiko bat lortuko duzu, eta bertan ikusiko duzu V eta t-ren erlazioa nolakoa den.

19. Zer ondorioztatzen duzu? Bete al da hipotesia?

Lehengoan gaudela ematen du. V eta t ez dira zuzenki proportzionalak ateratzen, hau da, V/t grafikoa zuzena da baina ez da jatorritik igarotzen. Eta lehen bezala, hori ere ez da hain arraroa. Grafikoa jatorritik igarota gasaren bolumenak V = 0 ml izan beharko luke bere tenperatura t = 0 °C denean. Eta zero azpiko tenperaturan bolumenak negatiboa izan beharko luke. Ez du zentzu handirik.
Hori ikusita, Gay-Lusacek gasaren bolumenak zerorantz zein tenperaturatan joko zukeen kalkulatu zuen. Horretarako, grafikoa luzatu egin zuen (benetako neurketarik ez zuen egin, ezin baitzituen hain tenperatura baxuak lortu ) eta -273 °C-ko tenperaturarentzat bolumena zero egingo zela ikusi zuen. Gainera, gas kantitate desberdinak erabiltzean lortutako grafikoak ez ziren berdinak baina antzeko itxura zeukaten: kasu guztietan, -273 °C-eko tenperaturan bolumenak zerorantz jotzen zuen.

20. Egiazta ezazu guk lortu dugun grafikoan ere hori betetzen dela, bolumenak zerorantz jotzen duela -273 °C-eko tenperaturan.

 

Beraz, tenperatura-eskalaren jatorria puntu horretara (-273 °C) eramanez, tenperatura-eskala absolutua erabiliz, bolumena ere zero egiten da tenperatura zero denean, V/T grafikoa jatorritik igarotzen den zuzena da, V eta T zuzenki proportzionalak dira: proposatutako hipotesia bete egiten da, alegia.
Hau da Gay-Lussac-en lehen legea:
Gas batek betetzen duen bolumena tenperatura absolutuarekiko zuzenki proportzionala da, presioa eta korpuskulu-kopurua konstante mantentzen badira:
V = k·T